Hierarchical Clustering (HCA)

Load Required Libraries

library(dendextend)
library(factoextra)

In the first part of this analysis, I build a random number x,y plot and store the vectors in a data frame. The first graph shows the plots of random vectors and I label them. The second table shows the Euclidean distance values for each point. The first dendrogram shows the clustered vectors.

set.seed(1234); par(mar=c(0,0,0,0)) #set graph margins
x <- rnorm(12, mean=rep(1:3, each=4), sd=0.2) #make random numbers 3 groups, 4 elements with means fo 1,2,3 standard dev=0.2
y <- rnorm(12, mean=rep(c(1,2,1), each=4),sd=0.2) #12 random numbers, 3 groups, 4 elements, means 1,2,1, standDev=0.2
plot(x,y, col="blue", pch=19, cex=2) #plot random numbers in a graph
text(x+0.05, y+0.05, label=as.character(1:12)) #label points

dataFrame <- data.frame(x=x, y=y) #store x,y info in a data frame.
dist(dataFrame, method="euclidean") #distance matrix default euclidean

##             1          2          3          4          5          6          7
## 2  0.34120511                                                                  
## 3  0.57493739 0.24102750                                                       
## 4  0.26381786 0.52578819 0.71861759                                            
## 5  1.69424700 1.35818182 1.11952883 1.80666768                                 
## 6  1.65812902 1.31960442 1.08338841 1.78081321 0.08150268                      
## 7  1.49823399 1.16620981 0.92568723 1.60131659 0.21110433 0.21666557           
## 8  1.99149025 1.69093111 1.45648906 2.02849490 0.61704200 0.69791931 0.65062566
## 9  2.13629539 1.83167669 1.67835968 2.35675598 1.18349654 1.11500116 1.28582631
## 10 2.06419586 1.76999236 1.63109790 2.29239480 1.23847877 1.16550201 1.32063059
## 11 2.14702468 1.85183204 1.71074417 2.37461984 1.28153948 1.21077373 1.37369662
## 12 2.05664233 1.74662555 1.58658782 2.27232243 1.07700974 1.00777231 1.17740375
##             8          9         10         11
## 2                                             
## 3                                             
## 4                                             
## 5                                             
## 6                                             
## 7                                             
## 8                                             
## 9  1.76460709                                 
## 10 1.83517785 0.14090406                      
## 11 1.86999431 0.11624471 0.08317570           
## 12 1.66223814 0.10848966 0.19128645 0.20802789

distxy <- dist(dataFrame)
hClustering <- hclust(distxy) #cluster the data
plot(hClustering) #plot to graph, see 3 main clusters
par(oma=c(2,2,2,2)) #reconfigure margins
par(mai=c(1,1,1,1))
plot(hClustering) #plot is more centered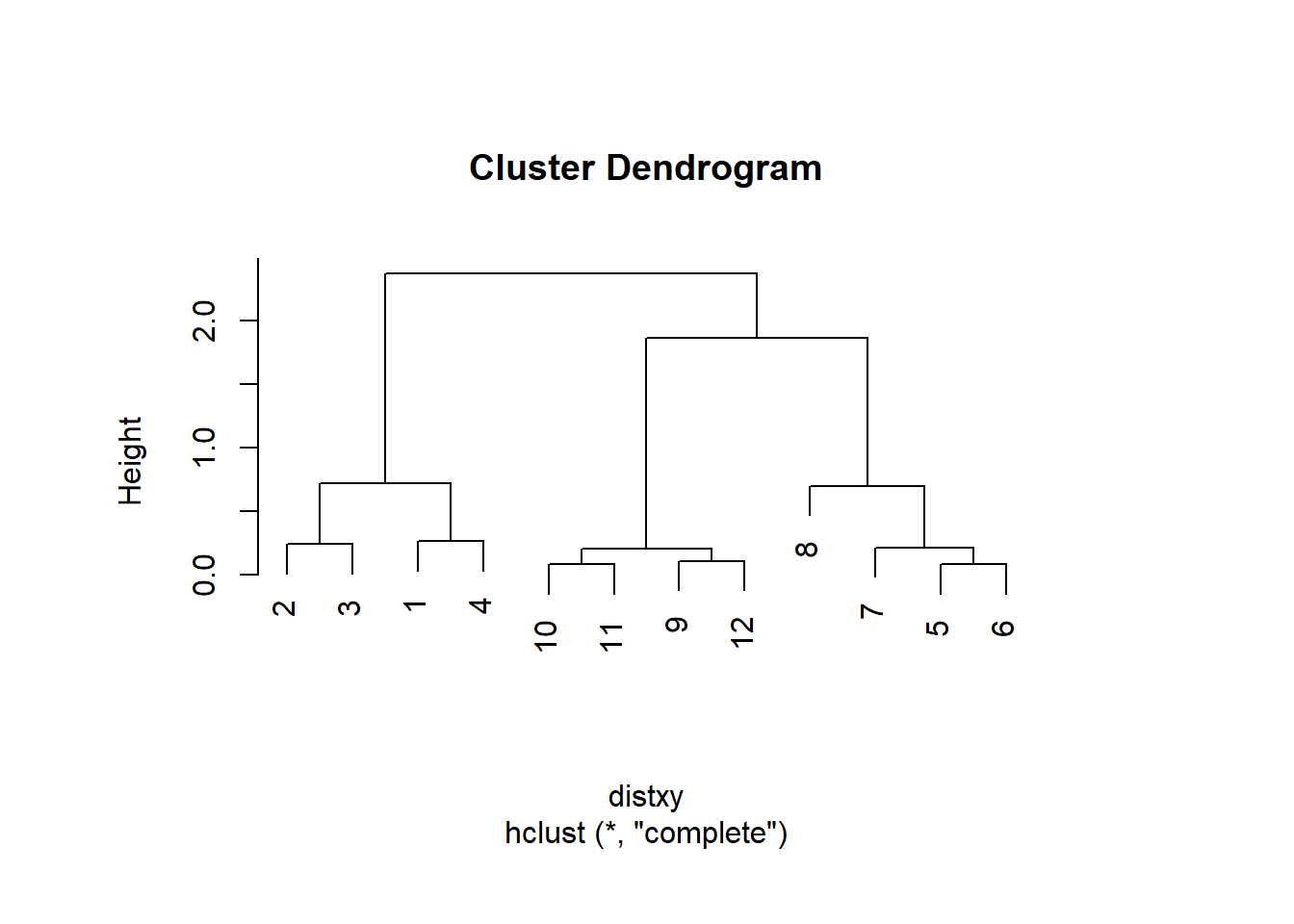

This next section shows basic coloring of the clusters and a rectangular box to enforce the three cluster regions.

#Add color Dendrogram 

dend <- dataFrame %>% 
  dist %>% 
  hclust %>% 
  as.dendrogram
dend %>% 
  color_branches(k=3) %>%
  plot(horiz=FALSE, main="Horizontal Dendrogram")
dend %>% 
  rect.dendrogram(k=3, horiz = FALSE)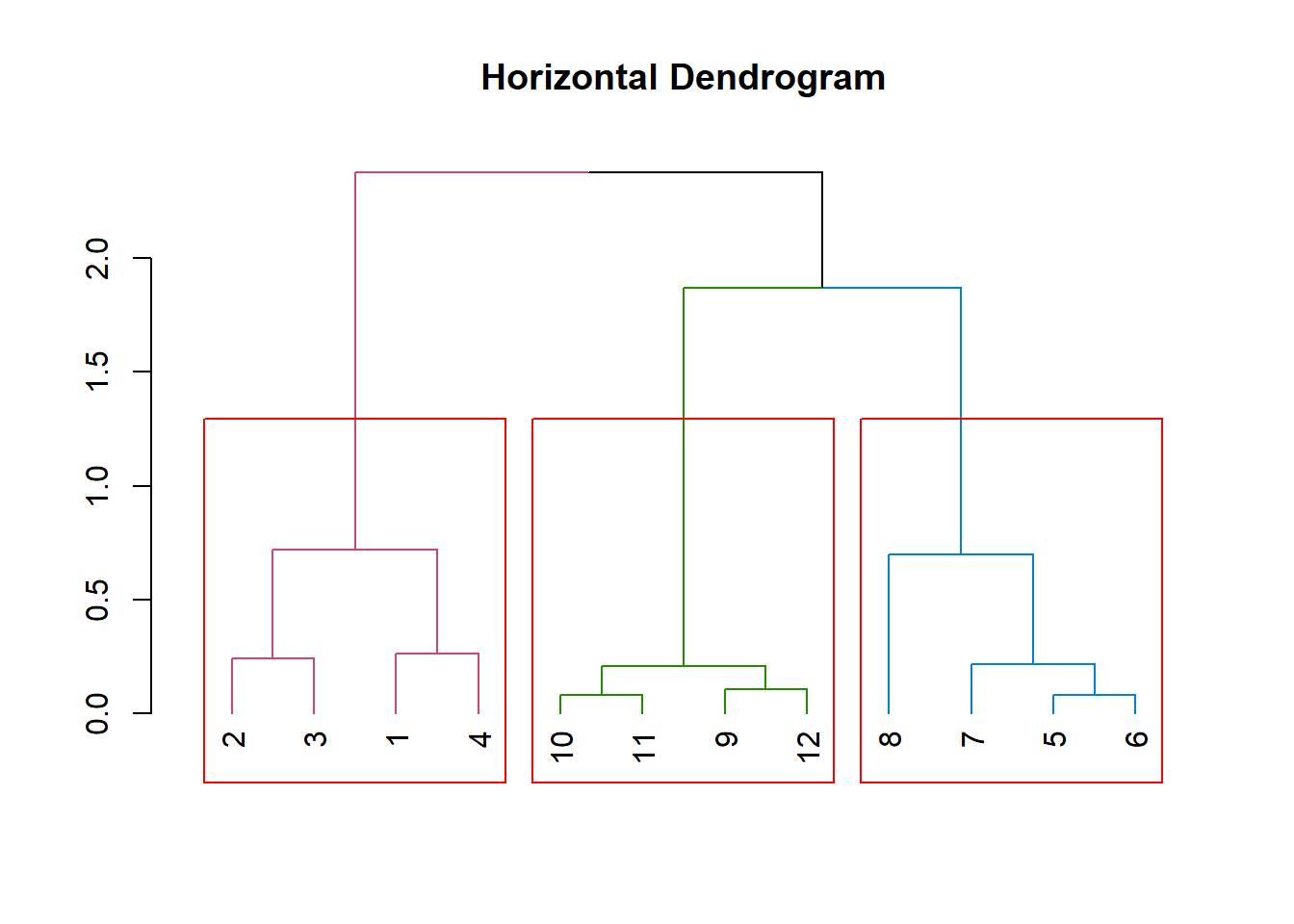

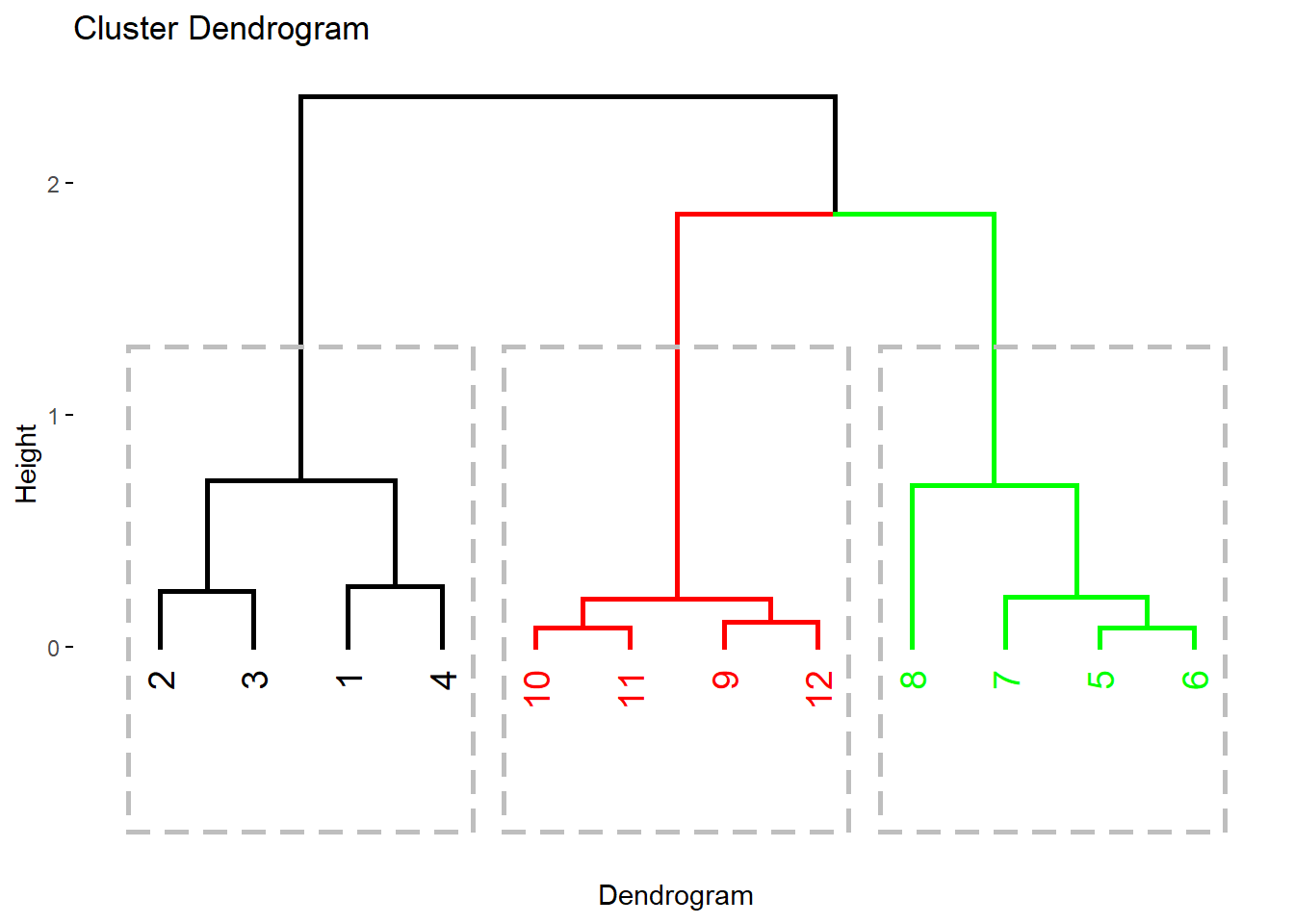
This graph shows a better visual for the three clusters with thicker lines and richer colors along with the outline rectangles around each cluster.

fviz_dend(dend, k=3, 
          cex=1, 
          k_colors=c("black", "red", "green"),
          color_labels_by_k = TRUE,
          lwd=1,
          rect =TRUE,
          xlab ="Dendrogram"
)

The code below becomes more complex and is the example from Exploratory Data Analysis. Here the dendrogram is only colored in the leaf labels 1,2,3. Great for grouping but vague because now we don’t know what cluster 1,2,3 mean regarding the variables.It just shows thee are 3 variables. The heat map was another example and in the graphic we can see what values are clustered together.

myplclust <- function( hclust, lab=hclust$labels, lab.col=rep(1,length(hclust$labels)), hang=0.1, ...){
  y <- rep(hclust$height, 2); x <- as.numeric(hclust$merge)
  y <- y[which(x<0)]; x <- x[which(x<0)]; x <- abs(x)
  y <- y[order(x)]; x <- x[order(x)]
  plot( hclust, labels=FALSE, hang=hang, ... )
  text( x=x, y=y[hclust$order] -(max(hclust$height)*hang),
        labels=lab[hclust$order], col=lab.col[hclust$order], 
        srt=90, adj=c(1,0.5), xpd=NA, ... )
}

dataFrame <- data.frame(x=x, y=y)
distxy <- dist(dataFrame)
hClustering <- hclust(distxy)
myplclust(hClustering, lab=rep(1:3, each=4), lab.col=rep(1:3, each=4))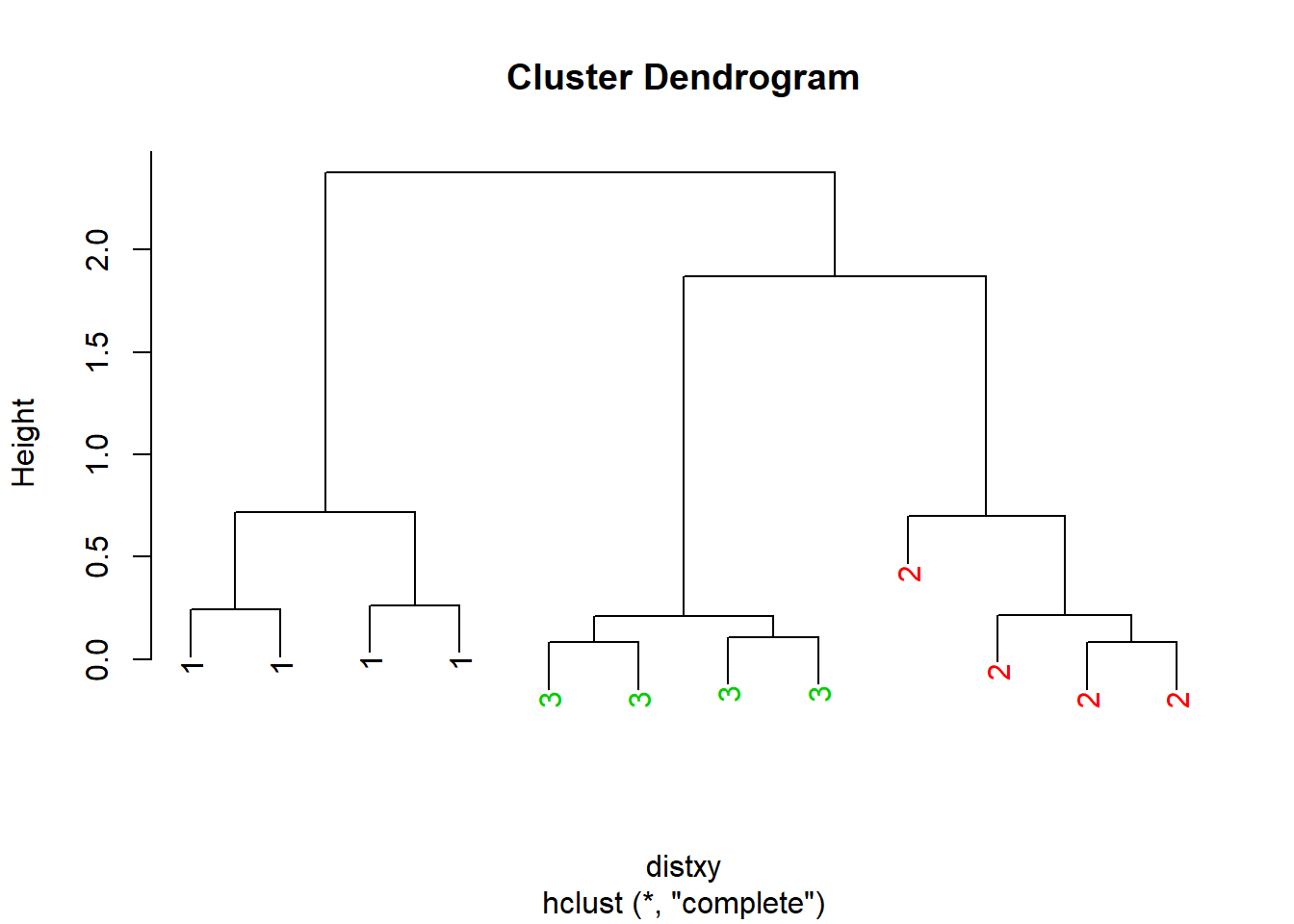

(143)

## [1] 143

dataMatrix <- as.matrix(dataFrame)[sample(1:12),]
heatmap(dataMatrix)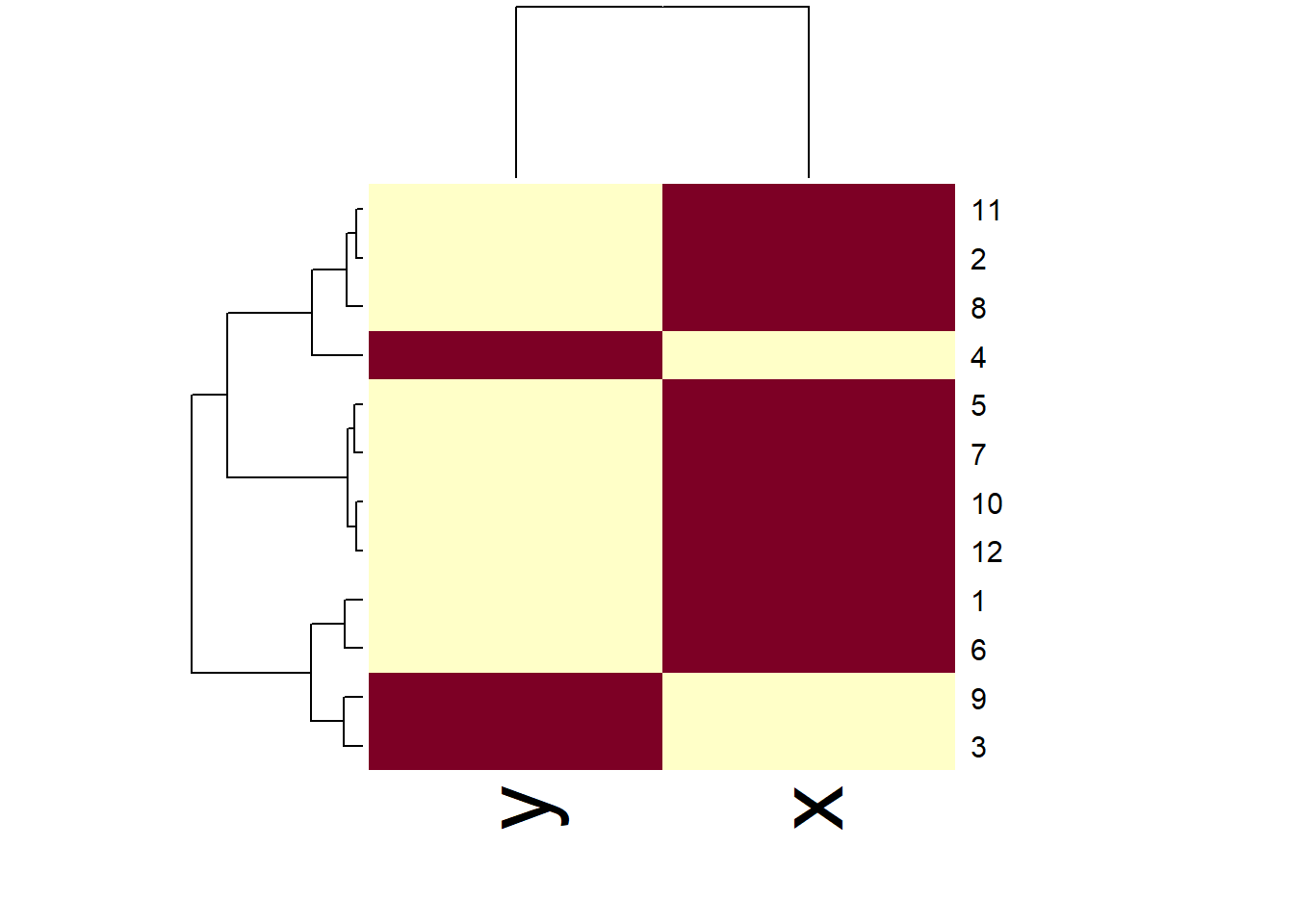

Below is the same dendrogram example from above and it was labeled on the x-axis and the leaves of each cluster are labeled 10,11,12 which again is not descriptive of the data points being represented. The color is set for each cluster again demonstrating a different color scheme. The parameters in the myplclust were adjusted to make these changes.

myplclust <- function( hclust, lab=hclust$labels, lab.col=rep(1,length(hclust$labels)), hang=0.1, ...){
  y <- rep(hclust$height, 2); x <- as.numeric(hclust$merge)
  y <- y[which(x<0)]; x <- x[which(x<0)]; x <- abs(x)
  y <- y[order(x)]; x <- x[order(x)]
  plot( hclust, labels=FALSE, hang=hang, ... )
  text( x=x, y=y[hclust$order] -(max(hclust$height)*hang),
        labels=lab[hclust$order], col=lab.col[hclust$order], 
        srt=90, adj=c(1,0.5), xpd=NA, ... )
}
myplclust(hClustering, lab=rep(10:12, each=4), lab.col=rep(3:5, each=4), xlab="Dendrogram", sub="Example")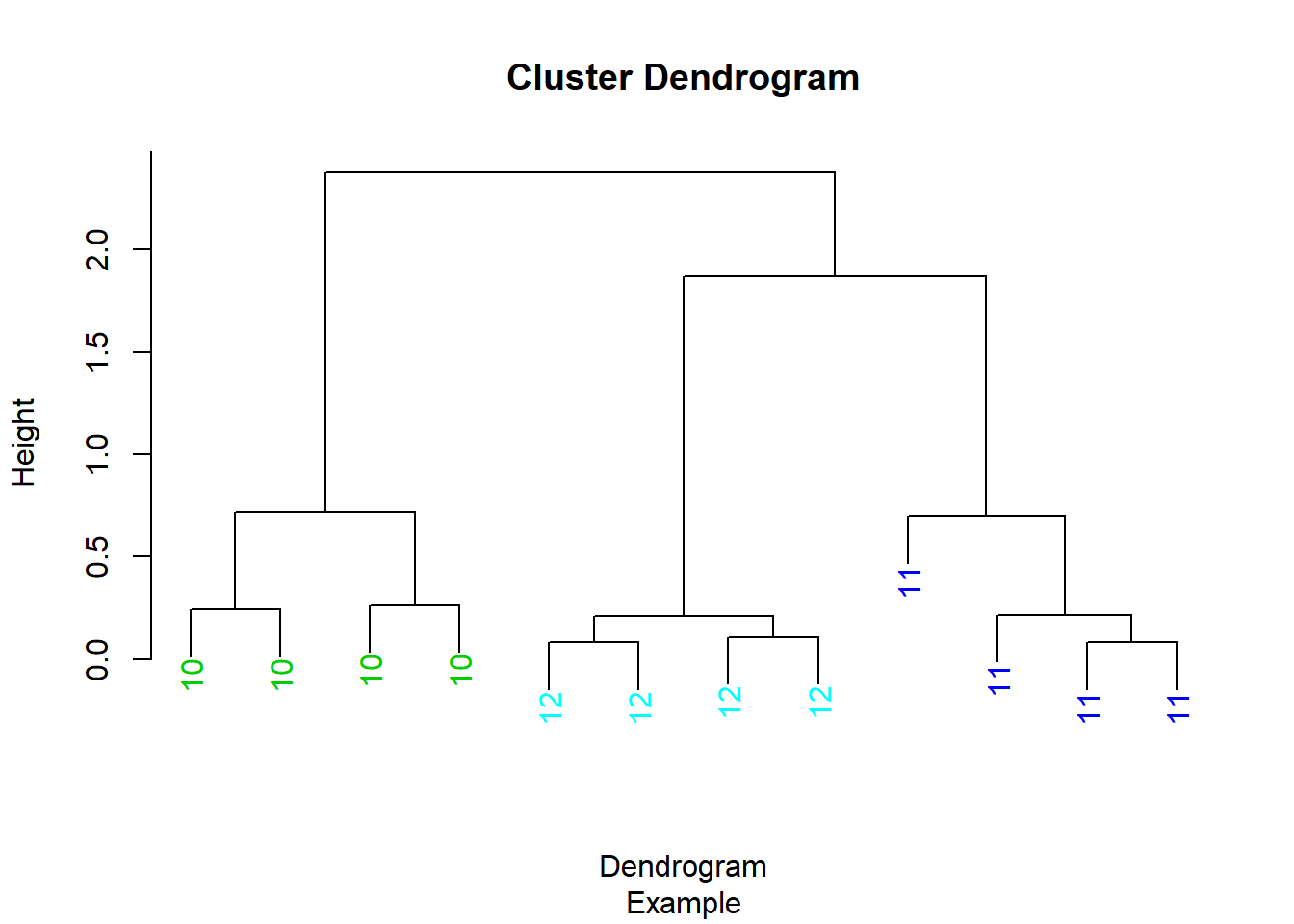

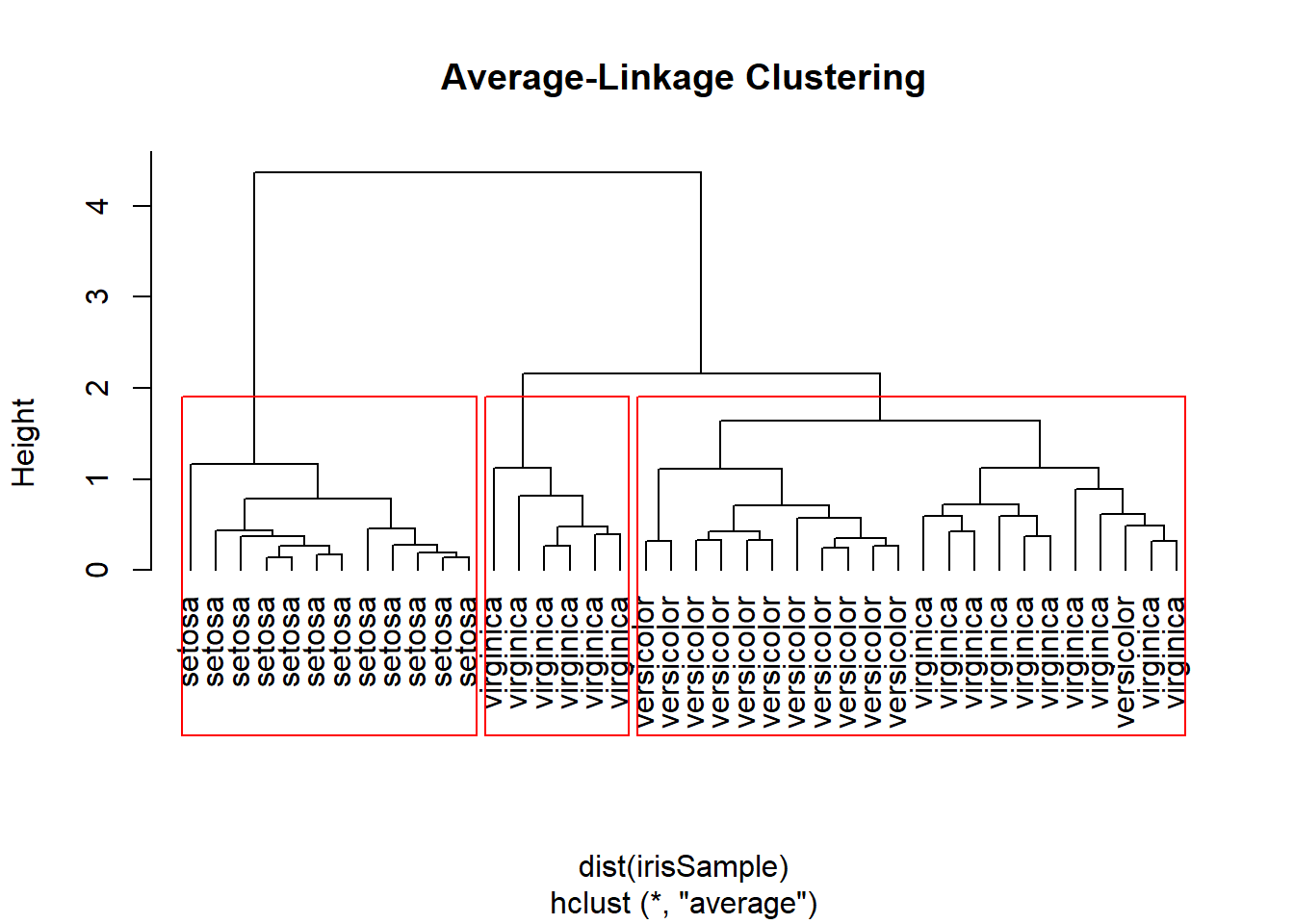
Avgerage Linkage Clustering Example

library(datasets)
set.seed(1234)
idx <- sample(1:dim(iris)[1],40)
irisSample <- iris[idx, ]
irisSample$Species <- NULL
hc <- hclust(dist(irisSample), method = "average")
plot(hc, hang=-1, labels=iris$Species[idx], main="Average-Linkage Clustering")
groups <- cutree(hc, k=3)
rect.hclust(hc, k=3)